你有没有想过，数学的世界里，有些函数就像追逐梦想的旅人，它们在数轴上奔跑，最终会汇聚到一个点，这个点就是它们的归宿——收敛点。今天，就让我们一起走进这个奇妙的世界，探索一下收敛函数的秘密吧！

什么是收敛函数？

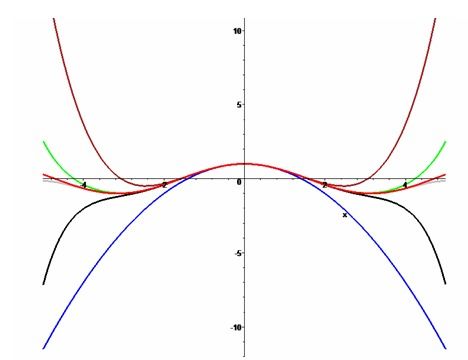
想象你手中有一根不断延伸的线，这根线代表了一个函数。随着你不断向前走，这根线会越来越靠近某个固定的点。这个固定的点，就是收敛函数的收敛点。简单来说，收敛函数就是那些在数轴上不断靠近某个点的函数。

收敛函数的诞生

收敛函数并不是凭空出现的，它们有着严格的定义。在数学的世界里，收敛函数的诞生往往与极限的概念紧密相连。当函数在某一点附近，无论你怎样靠近，函数的值都不会偏离一个固定的值太远，那么这个固定的值，就是函数在该点的极限。

收敛函数的类型

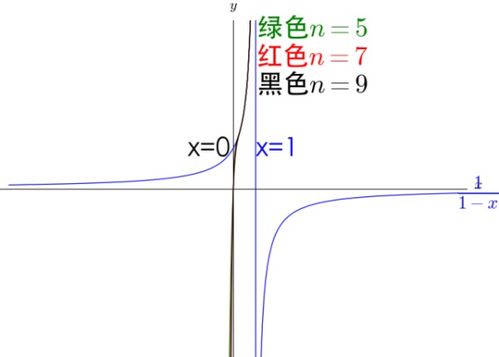
收敛函数有很多种，它们就像数学世界里的多彩花朵，各有各的特色。以下是一些常见的收敛函数类型：

1. 数列收敛：想象你有一串数字，这些数字一个比一个大，但它们之间的差距越来越小，最终会稳定在一个固定的值。这样的数字串，就是数列收敛。

2. 函数收敛：这就像我们刚才说的，函数在数轴上不断靠近某个点，这个点就是函数的收敛点。

3. 全局收敛：全局收敛的函数，无论你从哪个点开始，最终都会汇聚到同一个点。

4. 局部收敛：局部收敛的函数，只在某个特定的区域内收敛。

收敛函数的应用

收敛函数在数学、物理、工程等领域都有着广泛的应用。以下是一些例子：

1. 物理学：在物理学中，收敛函数可以用来描述粒子在空间中的运动轨迹。

2. 工程学：在工程学中，收敛函数可以用来分析电路中的电流和电压。

3. 经济学：在经济学中，收敛函数可以用来描述经济增长的趋势。

如何判断收敛函数

判断一个函数是否收敛，需要运用一些数学工具。以下是一些常用的方法：

1. 极限法：通过计算函数在某一点的极限，来判断函数是否收敛。

2. 级数法：将函数表示成一个级数的形式，然后判断级数的收敛性。

3. 泰勒级数法：将函数在某一点附近展开成泰勒级数，然后判断级数的收敛性。

收敛函数的符号解析

在数学的世界里，收敛函数有着一套独特的符号体系。以下是一些常见的符号：

1. lim：表示极限。

2. f(x)：表示函数。

3. x→a：表示x趋近于a。

4. L：表示极限值。

5. N：表示自然数。

这些符号组合在一起，就能帮助我们理解收敛函数的本质。

在这个充满奥秘的数学世界里，收敛函数就像一颗璀璨的明珠，闪耀着智慧的光芒。通过探索收敛函数，我们可以更好地理解数学的美丽和力量。让我们一起踏上这场奇妙的旅程，去发现更多数学的奥秘吧！